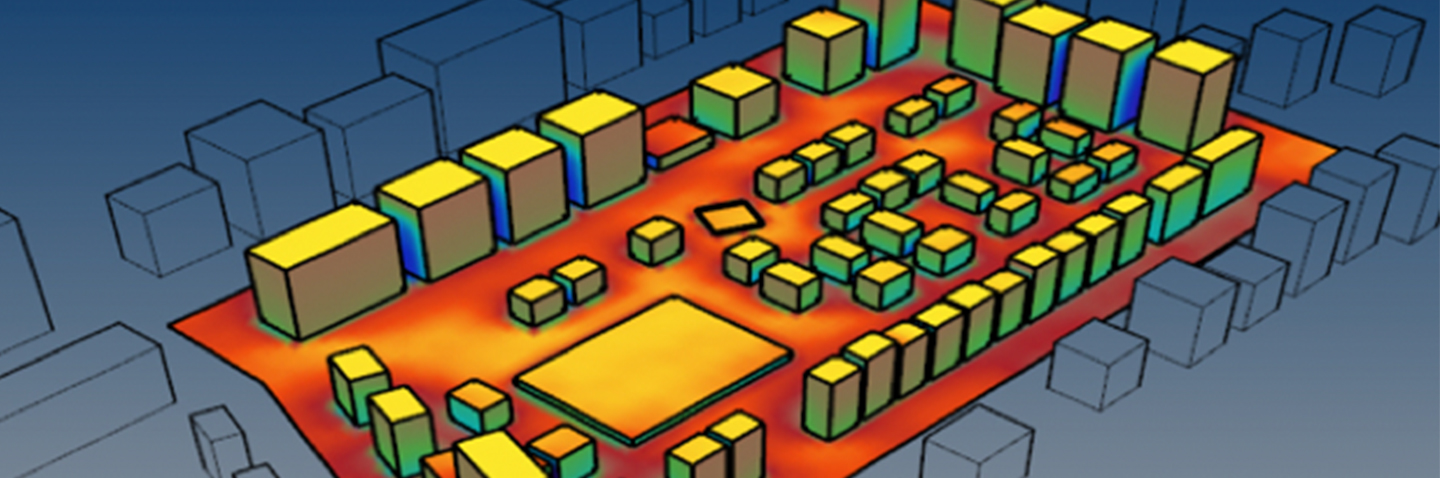
Entscheidungsunterstützung für die Stadtplanung

Ungekoppelte Stadthindernismodelle ersetzen die vollwertige atmosphärische Darstellung durch ein rechnerisch leichtes Äquivalent, das der Optimierung von Entwürfe der städtischen Gestaltung dient. Dieser Art von Modell können Randbedingungen aufgeprägt werden, die die Forschenden entweder durch Messungen oder eine mesoskalige Simulation gewinnen. Üblicherweise werten sie hierfür die Daten einer nahen Wetterstation im ländlichen Umland (z. B. eines Flughafens) aus. Um daraus schließlich die Randbedingungen abzuleiten, wird der Impuls- und Energieaustausch zwischen der Stadthindernisschicht und der umgebenden Atmosphäre vereinfacht dargestellt.

Das Stadthindernismodell bildet also die echte Stadtgeometrie als eine gleichwertige, vereinheitlichte Anordnung von Gebäuden und Straßen ab, die auf den durchschnittlichen morphologischen Parametern des realen Stadtgebiets basiert. Die hierbei zu berücksichtigenden, thermischen Wechselwirkungen finden hauptsächlich in der Luft in Straßenschluchten statt, da diese sowohl mit den bebauten Flächen als auch der freien Atmosphäre oberhalb der Stadthindernisschicht in Kontakt steht. Um diese Interaktionen darzustellen, kommt ein dynamisch-thermisches »lumped-parameter«-Netzwerkmodell zum Einsatz. Es bietet komplexe physikalische Modelle zum Erfassen der Aerodynamik und Evapotranspiration. Insgesamt läuft die Simulation für jede Stunde eines Standardjahres. Die wesentlichen Ergebnisse sind die durchschnittliche Energienutzung von Gebäuden sowie die Intensität der städtischen Wärmeinsel.

Bei entkoppelten Stadthindernismodellen ist zwischen zwei Hauptkategorien zu unterscheiden; der einschichtigen und mehrschichtigen. Der Fokus des einschichtigen Modells liegt auf dem Gesamtaustausch von Wärme, Impuls und Feuchtigkeit mit der Atmosphäre direkt oberhalb der Stadthindernisschicht. Dabei wird in den Straßenschluchten eine konstante Lufttemperatur und Luftfeuchtigkeit angenommen. Das mehrschichtige Modell wird typischerweise hinsichtlich der horizontal gemittelten Strömung und des skalaren Transports parametrisiert. Dieser Ansatz ermöglicht eine höhere Auflösung der atmosphärischen Prozesse, was jedoch mit einem größeren Rechenaufwand einhergeht.

Anwendungsbeispiele:

• Planung der Energieversorgung (Energieversorgungsunternehmen, Netzbetreiber)
• Wirkungsanalyse der urbanen Vegetation, Dach- und Wandbegrünung, Kühlflächen, Photovoltaik (nationale energiepolitische Entscheidungsträgerinnen und -träger)
• Optimierung der Stadtgestaltung (Stadtplanerinnen und -planer)
• Klimabewusste Gebäudeplanung (Architektinnen und Architekten sowie Gebäudeenergietechnikerinnen und -techniker).